Na₂CO₃溶液里究竟有什么？为什么它呈碱性？

如果你是初中生，你是否好奇过 \(\ce{Na2CO3}\) 溶液为什么呈碱性？如果你正在上高一，做题时是否好奇过 \(\ce{H2CO3}\)、\(\ce{HCO3-}\)、\(\ce{CO3^2-}\) 在水溶液中究竟有什么关系？这篇文章将尽力解答这些疑惑。

具备初中化学基础即可阅读本文。内容适合处于初中、高一的同学，也可作为高二化学的预习材料。

本文的内容不完全准确，但对初学者来说已经足够了。

预备知识

还记得相对分子质量的定义吗？

约定：拥有 \(6\) 个质子 \(6\) 个中子的碳原子 \(\ce{^{12}C}\) 的相对分子质量为 \(12\)，并由此推出其它元素/物质的相对分子质量。

自然地，我们可以问这样一个问题：多少个 \(\ce{^{12}C}\) 的质量恰好是 \(12g\) 呢？这个数字比你想象的大得多，大概是 \(6.02 \times 10^{23}\) 个。

这样我们也可以说：

• 因为 \(\ce{H}\)（原子）的相对分子质量是 \(1\)，所以 \(6.02 \times 10^{23}\) 个 \(\ce{H}\) 原子的质量是 \(1g\)。
• 因为 \(\ce{H2}\)（分子）的相对分子质量是 \(2\)，所以 \(6.02 \times 10^{23}\) 个 \(\ce{H2}\) 分子的质量是 \(2g\)。
• 因为 \(\ce{CaCO3}\) 的相对分子质量是 \(100\)，所以 \(6.02 \times 10^{23}\) 个 \(\ce{CaCO3}\) 分子的质量是 \(100g\)。

每次都要说这么大一坨数字是很麻烦的，于是我们这样定义一个叫作 \(mol\) 的单位：

\[1mol = 6.02 \times 10^{23} \text{个}\]

这样，就可以简单地表述为：\(1mol\ \ce{CaCO3}\) 的质量是 \(100g\)，\(0.5mol\ \ce{CaCO3}\) 的质量是 \(50g\)。

或者：\(\ce{CaCO3}\) 的摩尔质量是 \(100g/mol\)

注意，这和“\(\ce{CaCO3}\) 的相对分子质量是 \(100\)”本质上没有任何区别，不要被新的单位与符号吓到。

那么为什么要玩这些文字游戏呢？我们明明可以继续说“\(\ce{CaCO3}\) 的相对分子质量是 \(100\)”。看起来完全没有必要引入 \(mol\) 这样一个单位，并且发明“\(\ce{CaCO3}\) 的摩尔质量是 \(100g/mol\)”这句话呀！

这是因为，我们在研究化学中，很多时候需要关注的微粒的数量（具体的例子将在后文出现）。分子尺度的东西很小，哪怕是看起来一点点，个数也会很大。“瓶子里有 \(9.03 \times 10^{23}\) 个 \(\ce{CaCO3}\) 分子”相比于“瓶子里有 \(1.5mol\ \ce{CaCO3}\)”显得过于臃肿。

因此，引入 \(mol\) 很重要的一个原因，就是让我们讨论数量时使用的数值不至于太大。而选择 \(1mol\) 对应 \(6.02 \times 10^{23}\) 个（而非其它类似 \(1 \times 10^{24}\) 这样的数字），则是为了让 \(g/mol\) 在数值上恰好与相对分子质量相等。

通过“改变比例尺”定义新单位有两个动机/好处

• 让日常使用时数值不太大也不太小
• 让某些情境下的数字/公式长得好看

这种“量身定制”在数学中也会遇到：使用弧度制表示角。此处不过多说明。

浓度

初中时，我们会用单位 \(g/L\)（即某种微粒在单位体积水中的质量）来表示微粒在水中的浓度。

正如前文所说，有时更重要的是个数而非质量，所以我们也会用 \(mol/L\) 来表示微粒在水中的浓度。

为了区分，我们把 \(g/L\) 称为质量浓度，把 \(mol/L\) 称为摩尔浓度。

本文所指的浓度都是摩尔浓度，高中阶段也通常只使用摩尔浓度。

此外，本文约定使用“中括号包裹物质”来指代物质在水中的浓度。例如 \([\ce{Ca^2+}]\) 表示水溶液中 \(\ce{Ca^2+}\) 的浓度。

一瓶纯水里有什么？

从现在开始，假设我们处于 \(25^\circ C\) 的舒适学习环境 :D

你需要知道这几个初中时未接触过的基本事实：

• 纯水并不是完全由一个个 \(\ce{H2O}\) 分子构成的，里面还会存在少量且等量的 \(\ce{H+}\) 和 \(\ce{OH-}\)。
• 水溶液中一定会同时存在 \(\ce{H+}\) 和 \(\ce{OH-}\) 两种离子。所谓“中性”就是二者数量相等，所谓“酸性”就是 \(\ce{H+}\) 数量多于 \(\ce{OH-}\)，酸性/碱性强弱反映的则是指二者之间的浓度差异到底有多大。

既然二者可以共存，为什么还会发生酸碱中和反应呢？因为二者只是不能大量共存。

水中存在一个可以向两个方向进行的反应（即可逆反应）

\[\ce{H2O <=> H+ + OH-}\]

这个反应也叫做水的电离平衡。

当溶液中 \(\ce{H+}\) 和 \(\ce{OH-}\) 太多时，反应向左进行，部分 \(\ce{H+}\) 与 \(\ce{OH-}\) 结合成 \(\ce{H2O}\)，即酸碱中和。
当溶液中 \(\ce{H+}\) 和 \(\ce{OH-}\) 太少时，反应向右进行，部分 \(\ce{H2O}\) 分解成 \(\ce{H+}\) 与 \(\ce{OH-}\)，即水的电离。

从定量的角度，大自然就像一个精准而神奇的机器，总会通过调整可逆反应的方向保证水中 \(\ce{H+}\) 和 \(\ce{OH-}\) 浓度满足这样的定量关系：

\[[\ce{H+}]\cdot[\ce{OH-}]=1 \times 10^{-14}\ mol^2\cdot L^{-2}\]

因此，纯水中 \(\ce{H+}\) 和 \(\ce{OH-}\) 的浓度都是 \(1 \times 10^{-7}\ mol/L\)，纯水呈中性。

现在我们已经研究透了纯水，是时候看看往纯水里加点东西会发生什么了！

当我们往 \(1L\) 纯水中加入 \(1mol\ \ce{NaOH}\) 固体时， \(\ce{NaOH}\) 溶解于水中电离为 \(\ce{Na+}\) 和 \(\ce{OH-}\)，此时水中 \([\ce{H+}]=1 \times 10^{-7}\ mol/L\)，\([\ce{OH-}] = (1 \times 10^{-7} + 1)\ mol/L\)。

二者乘积变得显著大于 \(1 \times 10^{-14}\)，因此水的电离平衡将向左进行，水中 \(\ce{H+}\) 和 \(\ce{OH-}\) 结合，同时减少，直到二者乘积回到 \(1 \times 10^{-14}\)。

为了方便后文指代，省略 \(1 \times 10^{-14}\ mol^2\cdot L^{-2}\) 的单位，并且约定 \(K_w=1 \times 10^{-14}\)。
\(K_w\) 也被称为水的电离平衡的平衡常数。

二者的减少量都很小，因为 \([\ce{H+}]\) 只减少一点就可以足够接近 \(0\)，使二者乘积迅速回到 \(K_w\)。由于 \([\ce{H+}]\) 不可能减少到 0，且根据反应方程式 \([\ce{H+}]\) 与 \([\ce{OH-}]\) 减少量相同，所以减少后 \([\ce{OH-}]\) 应当在 \(1\ mol/L\) 到 \((1 \times 10^{-7} + 1)\ mol/L\) 之间。

一瓶 \(\ce{Na2CO3}\) 溶液里有什么？

所谓 \(\ce{Na2CO3}\) 溶液，就是将 \(\ce{Na2CO3}\) 固体溶于水中得到的溶液。（这句话看起来很显然很愚蠢，但也只是看起来）

\(1mol\ \ce{Na2CO3}\) 固体溶于水中，电离为 \(2mol\ \ce{Na+}\) 和 \(1mol\ \ce{CO3^2-}\)。这显然并不会给溶液带来酸碱性的变化，可是我们已经知道 \(\ce{Na2CO3}\) 溶液呈碱性，这是为什么呢？

\(\ce{H2CO3}\)、\(\ce{HCO3-}\)、\(\ce{CO3^2-}\) 其实是三个不同的微粒（这在初中时是没有被强调的），水中如果存在它们中的某一个，那么一定也会同时存在另外两个，只不过浓度差异可能很大。具体的定量关系是这样被确定的：

\[ \displaylines{ \ce{H2CO3 <=> H+ + HCO3-}\qquad (1)\\ \frac{[\ce{H+}]\cdot[\ce{ HCO3-}]}{[\ce{H2CO3}]}=4.5 \times 10^{-7} } \]

\[ \displaylines{ \ce{HCO3- <=> H+ + CO3^2}\qquad (2)\\ \frac{[\ce{H+}]\cdot[\ce{ CO3^2-}]}{[\ce{HCO3-}]}=4.7 \times 10^{-11} } \]

为了后文表述方便，令 \(K_{a1}=4.5 \times 10^{-7}\)、\(K_{a2}=4.7 \times 10^{-11}\)
此处 \(K_{a1}\) 也被称为 \(\ce{H2CO3}\) 第一级电离的平衡常数；\(K_{a2}\) 也被称为 \(\ce{H2CO3}\) 第二级电离的平衡常数，或者 \(\ce{HCO3-}\) 电离的平衡常数

不妨以 \(1mol\ \ce{Na2CO3}\) 固体溶于 \(1L\) 纯水中为例，看看会发生什么。

\(1 mol\ \ce{Na2CO3}\) 溶于 \(1L\) 水后水中各微粒浓度：

\[ \displaylines{ [\ce{H+}] = 1 \times 10^{-7} mol/L\\ [\ce{OH-}] = 1 \times 10^{-7} mol/L\\ [\ce{CO3^2-}] = 1 mol/L\\ [\ce{Na+}] = 2 mol/L } \]

为了简化分析，我们先假设反应 \((1)\) 不存在。

考虑反应 \((2)\)，由于溶液中还没有 \(\ce{HCO3-}\)，所以反应 \((2)\) 肯定会向左进行，使溶液中 \([\ce{CO3^2-}]\)、\([\ce{H+}]\) 减小，\([\ce{HCO3-}]\) 由 \(0\) 增大，直到溶液中 \(\frac{[\ce{H+}]\cdot[\ce{ CO3^2-}]}{[\ce{HCO3-}]}=K_{a2}\)。

不要忘记，这个过程中 \([\ce{H+}]\) 的减小会导致 \([\ce{H+}]\cdot[\ce{OH-}]\) 变得小于 \(K_w\)，所以水的电离平衡会向右反应，部分 \(\ce{H2O}\) 电离为 \(\ce{H+}\) 和 \(\ce{OH-}\)，直到 \([\ce{H+}]\cdot[\ce{OH-}]=K_w\)。由于 \([\ce{OH-}]\) 是从 \(1 \times 10^{-7}mol/L\) 开始增大，所以最终结果一定是 \([\ce{OH-}] > 1 \times 10^{-7}mol/L > [\ce{H+}]\)，按照前文对酸碱性的定义，溶液是呈碱性的。

实际上，神奇的大自然就像是是在解关于 \([\ce{H+}]\)、\([\ce{OH-}]\)、\([\ce{HCO3-}]\)、\([\ce{CO3^2-}]\) 四元方程组（尽管这样一个方程组对于人类大脑来说是不可解的）：

\[ \begin{equation*} \begin{cases} \frac{[\ce{H+}]\cdot[\ce{ CO3^2-}]}{[\ce{HCO3-}]}=K_{a2} \\ [\ce{H+}]\cdot[\ce{OH-}]=K_w \\ [\ce{HCO3-}] + [\ce{CO3^2-}] = 1mol/L \\ [\ce{HCO3-}] + 2[\ce{CO3^2-}] + [\ce{OH-}] = [\ce{Na+}] + [\ce{H+}] \end{cases} \end{equation*} \]

其中 \([\ce{Na+}]\) 保持 \(2 mol/L\) 不变
第三行等式是因为无论反应如何进行，水中碳元素总量都应保持不变，即含碳元素的微粒总浓度保持为最初的 \(1 mol/L\)
第四行等式也是无论反应如何进行，最终会有的必然结果，此处不作说明，感兴趣的读者可自己查询电荷守恒

所有反应完成后各微粒的浓度就是上面的方程组的解。

现在我们把化学方程式 \((1)\) 也考虑在内，像刚才那样的分析会变得非常复杂，不妨直接看看大自然实际上解的这个五元方程组：

\[ \begin{equation*} \begin{cases} \frac{[\ce{H+}]\cdot[\ce{ HCO3-}]}{[\ce{H2CO3}]}=K_{a1} \\ \frac{[\ce{H+}]\cdot[\ce{ CO3^2-}]}{[\ce{HCO3-}]}=K_{a2} \\ [\ce{H+}]\cdot[\ce{OH-}]=K_w \\ [\ce{H2CO3}] + [\ce{HCO3-}] + [\ce{CO3^2-}] = 1mol/L \\ [\ce{HCO3-}] + 2[\ce{CO3^2-}] + [\ce{OH-}] = [\ce{Na+}] + [\ce{H+}] \end{cases} \end{equation*} \]

通过计算机，我们可以得到解为：

\[ \begin{aligned} &\\ [\ce{H+}] &= 6.90583 \times 10^{-13}\ mol/L\\ [\ce{OH-}] &= 0.0144805\ mol/L\\ [\ce{CO3^2-}] &= 0.985519\ mol/L\\ [\ce{HCO3-}] &= 0.0144805\ mol/L\\ [\ce{H2CO3}] &= 2.22222 \times 10^{-8}\ mol/L \end{aligned} \]

此时溶液 \(pH \approx 12.2\)

如果最初投入的 \(\ce{Na2CO3}\) 溶于水后浓度不是 \(1 mol/L\)，第四行方程的数值 \(1mol/L\) 以及第五行方程的 \(\ce{[Na+]}\) 会发生改变，从而最终的解不同。

由此可见，\(\ce{Na2CO3}\) 水溶液呈碱性并不是什么神奇的事，只是大自然解一个方程组的结果。

最后回忆一下这一节的第一句话。将 \(1 mol\ \ce{Na2CO3}\) 固体溶于 \(1L\) 水中得到的溶液叫作 \(1 mol/L\ \ce{Na2CO3}\) 溶液，尽管溶液中 \(\ce{CO3^2-}\) 浓度只有大约 \(0.986 mol/L\)，并且存在极少的 \(\ce{H2CO3}\) 和一点 \(\ce{HCO3-}\)。

思考题

\(0.01 mol/L\ \ce{H2CO3}\) 溶液是什么？

根据上面的原理，想一想为什么 \(\ce{H2CO3}\) 溶液呈酸性。尝试像上文分析 \(1 mol/L\ \ce{Na2CO3}\) 溶液一样列出五元方程组，有几行方程需要改动？

总结

以上这些原理被叫做化学平衡，你将在高二进行详细的学习，到时候你在初中和高一的很多疑问都会得到解答。

关于化学平衡，最重要的精神是：没有什么反应是只能朝一个方向进行的，没有什么微粒是完全不存在的，区别只在于反应的难易程度以及最终微粒的数量差异，一切都只是大自然巧妙地解出复杂的方程组后的结果。

所以，当你在将来的学习中看到类似 “\(\ce{Na2CO3}\) 呈碱性” 这样的话时，请安心地接受它，因为你已经初步了解了这背后的原理，知道这没有什么神奇的，只不过是解一个方程组后得到的必然结果罢了。

类似地，这些话将在高一经常出现，它们背后其实也都遵循着非常统一的化学平衡原理。

• 强酸容易制弱酸
• 易溶沉淀容易转化为难溶沉淀
• \(\ce{CO2}\) 与 \(\ce{Na3CO3}\) 反应生成 \(\ce{NaHCO3}\)，但 \(\ce{CO2}\) 不与 \(\ce{NaHCO3}\) 反应
• “xxx 与少量 yyy 反应”、 “xxx 与过量 yyy 反应” 的方程式可能不同，甚至有的相同，有的不同
• \(\ce{Fe^3+}\) 只能存在于强酸性环境，弱酸/中性/碱性环境会变成 \(\ce{Fe(OH)3}\) 沉淀
• 明矾净水的原理与 \(\ce{Al3+}\) 水解生成 \(\ce{Al(OH)3}\) 有关
• 制备 \(\ce{Fe(OH)3}\) 胶体时一会出现 \(\ce{FeCl3 + 3H2O = Fe(OH)3(\text{胶体}) + 3HCl}\)，滴加 \(\ce{HCl}\) 溶解胶体时又出现 \(\ce{Fe(OH)3 + 3HCl = FeCl3 + 3H2O}\)。两个方程式仿佛是矛盾的。
• ……

本文介绍的原理不足以时你理解高一时遇到的这些现象，最合适的做法有两个：

• 如果你想彻底弄明白“为什么”，那就去提前系统地学习高二化学（人教版选择性必修一：化学反应原理）。
• 否则，请在高一时怀着「我知道这背后存在某些原理，并且我将在高二学习这些原理」的心态，安心地接受并背下这些结论。高二学完并深刻理解相关原理后，这么多难以记忆的结论将变成“显然”。

附：疑问解答

这里是对阅读过程中可能产生的疑问的解答。如果你还有疑问，欢迎在评论区提出。

Q：初中时学的 \(\ce{H2CO3 = 2H+ + CO3^{2-}}\) 是怎么回事？

这当然是不准确的，在高中阶段如果还这样理解就会在题目中饱受困扰。你需要拥有本文的介绍的知识，即水中 \([\ce{H2CO3}]\)、\([\ce{HCO3-}]\)、\([\ce{CO3^2-}]\) 一定会同时存在，数量是完全由几个方程决定的。（当然，浓度很小时可以近似认为不存在）

事实上，通过计算机可以算出溶液 \(pH\) 与溶液中三种微粒所占比例的关系：

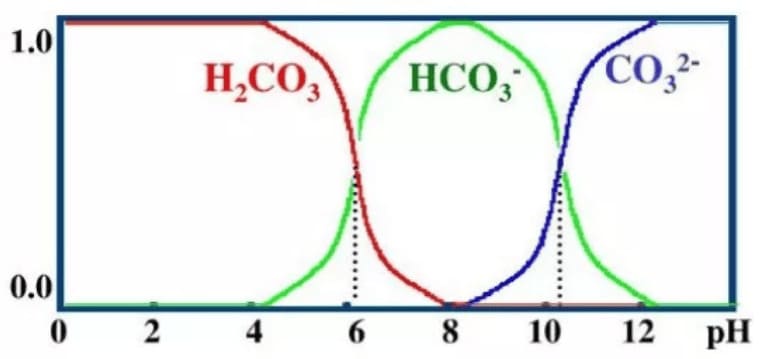
Q：\(\ce{H2CO3}\) 的电离 \(\ce{H2CO3 <=> H+ + HCO3}\) 是可逆反应，那 \(\ce{NaOH}\) 呢？如果 \(\ce{NaOH}\) 电离成为 \(\ce{Na+}\) 和 \(\ce{OH-}\) 也是可逆反应，难道不会对上面的分析产生影响吗？

严格来说，\(\ce{NaOH -> Na+ + OH-}\) 确实也是可逆的，但反应平衡时 \(\frac{[\ce{Na+}]\cdot[\ce{OH+}]}{[\ce{NaOH}]}\) 的数值非常大（有资料称在 \(10^{20}\) 附近，未仔细查证）。这就意味着，溶液中剩余的未电离的 \(\ce{NaOH}\) 浓度作为分母，应当极小。因此可以认为 \(\ce{NaOH}\) 在水中就是完全电离成 \(\ce{Na+}\) 和 \(\ce{OH-}\) 的，不用考虑其电离平衡向左反应。

Q：我听说过“强酸”“弱酸”“强碱”“弱碱”这些词，这和这篇文章提到的原理有关吗？

有的，当然有的。

所谓强酸强碱，就是其对应的电离平衡常数（也就是前文的 \(K\)，不同酸、碱的 \(K\) 不同）非常大，可以认为它们在水中完全电离为离子。
弱酸弱碱则需要考虑其电离平衡，正如前文对弱酸 \(\ce{H2CO3}\) 电离产物 \(\ce{CO3^2-}\) 的分析。

高中常见的强酸有 \(\ce{H2SO4}\)、\(\ce{HCl}\)、\(\ce{HNO3}\)、\(\ce{HI}\)、\(\ce{HBr}\)、\(\ce{HClO4}\)
高中常见的强碱有 \(\ce{KOH}\)、\(\ce{NaOH}\)、\(\ce{Ca(OH)2}\)、\(\ce{Ba(OH)2}\)

此外，如果你在高一时还遇到了各种关于高中化学的疑问，也欢迎在评论区提出。